2018 Jan - On Sharpening Pencils - Minimizing the waste of pencil sharpening
Wooden pencils are good for their simplicity and reliablility, but a lot of lead gets wasted from repeatedly sharpening the dull rod of lead into a cone. Of course, a mechanical pencil is able to use almost all of its lead payload, but these writing utensils can be heavier or flimsy. Determining how to best prolong the life of a traditional wooden pencil is very practical, and will also show how close in efficiency they can come to their mechanical counterparts. The specific questions to answer are:
- How dull should you use a pencil for until sharpening? And then,
- How sharp should you sharpen it, if not all the way?
The input parameters are the diameter of pencil lead, and angle of the conical tip when sharpened. The objective is to maximize the volume of lead used per length of lead.
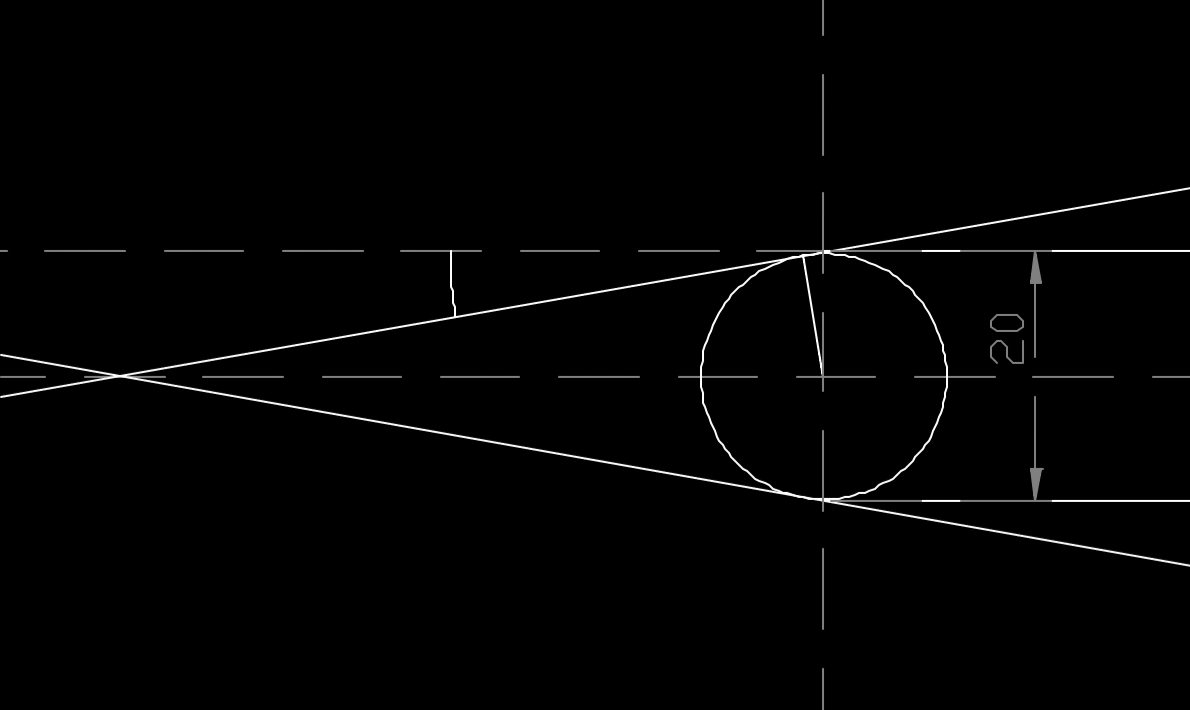
A CAD drawing is shown of the pencil lead. It shows the point of the pencil when it is sharp, and the rounded (assumed circular) end when dull. By looking at the geometry, it seems that keeping the pencil as dull as possible may actually waste the least amount of lead. Becasue when the tip is dull, sharpening it a little only removes a ring of lead, yet still reduces the diameter of the tip. If sharpened as little, but as often as possible, then this theoretically would waste no lead at all (the sharpness is maintained). However, the shape of the tip would tend towards a flat face, with sharpening serving the sole purpose of merely removing the wood so that the lead is exposed.
Even is this is true, it's not very useful; some sharpness is needed. Although, that makes things interesting: there must be a compromise. To keep things from getting subjective, the problem of "how sharp is sharp enough" will be avoided.
First, let's consider sharpening the pencil to a point. If sharpened too often, then only a small cylindrical core of lead will be used for writing, since the edges of the lead are always sharpened before it can be used. If sharpened too seldom, then large conical chunks will be wasted. Perhaps there is a sweet-spot.
To solve this problem, expressions for volume will be found by integrating across parts of the lead cross-section for different stages of sharpness, revovling around the central axis. The efficiency of lead used per length of lead dulled can be graphed to give a sense of the problem.
In the above paragraph, the realization that the tip will slowly become a flat face (if the sharpness is attempted to be maintained) breaks the assumption that the tip will always be spherical. It is becoming increasingly important to understand how the lead of the pencil wears away, since the shape will later determine how much sharpening is required.
To determine what parts wear first and the resulting shape, it will be assumed that the lead will always tend towards the smallest sphere that fits within the volume of remaining lead. It does not matter how fast the lead wears away; all that is needed to calculate waste is the resulting volume and usage ratios.
To be continued...
Testing TeX formula formatting: \(V_{cone} = {1 \over 3} \pi h r^2 \)
\( V_{sphere} = {{4 \over 3} \pi r^3} \)
Add formulas to HTML with MathJax
Also do: how long to use for if sharpening all the way is required
Then take all methods of waiting until extremes and find waste percentage, and compare