Observation of three-photon bound states in a quantum nonlinear medium

Bound states of light quanta have been proposed to exist in specifically engineered media with strong optical nonlinearities (1–5). Recently photonic dimers have been observed experimentally (6). Such bound states of photons can be viewed as quantum solitons (7, 8), which are shape-preserving wave-packets enabled by the cancellation of nonlinear and dispersive effects. In contrast to classical solitons where the self-consistent shape varies smoothly with total pulse energy, in a quantum soliton the optical nonlinearity is so strong that the wave packet shape depends on the constituent number of photons in a quantized manner (7,8). The creation of quantum solitons not only represents an important step in fundamental studies of photonic quantum matter (6, 9, 10), but also may enable new applications in areas ranging from quantum communication to quantum metrology (11,12).

We search for a photonic trimer using an ultracold atomic gas as a quantum nonlinear medium. This medium is experimentally realized by coupling photons to highly excited atomic Rydberg states by means of electromagnetically induced transparency (EIT). The resulting hybrid excitations of light and matter – Rydberg polaritons – inherit strong interactions from their Rydberg components, and can propagate with very low loss at slow group velocity v_g (13–15). The nonlinearity arises when photons are within a Rydberg blockade radius r_B of one another, where strong interactions between atoms in the Rydberg state (16) shift the Rydberg level out of the EIT resonance, blocking the excitation of more than one Rydberg atom within r_B. In the dissipative regime (on atomic resonance), the blockade results in photon loss and anti-bunching (17–19). In the dispersive, off-resonant regime, the index of refraction varies with the separation between photons, resulting in an attractive force (6).

Our experimental setup (20) (Fig. 1A, B) consists of a weak quantum probe field at λ=780 nm and waist w=4.5 μm coupled to the 100S_1/2 Rydberg state via a strong 479 nm control field in the EIT configuration (see Fig. 1B). The interactions occur in a cloud of laser-cooled ⁸⁷Rb atoms in a far-detuned optical dipole trap. Measurements are conducted at a peak optical depth 0DB ⋍ 5 per blockade radius r_B = 20 μm. To suppress dissipative effects, we work at large detuning Δ ≥ 3Γ from atomic resonance (Γ is the population decay rate of the 5P_3/2 state, see Fig. 1B), and at a control laser Rabi frequency where the transmission through the medium is the same with and without EIT, but the phase differs appreciably (Fig. 1C). Consequently, the transmission hardly varies with probe photon rate (Fig. 1D top), while a strongly rate-dependent phase with a slope of 0.40(7) rad·μs is observed (Fig. 1D bottom).

The quantum dynamics of interacting photons are investigated by measuring the three-photon correlation function and phase. Because dispersion outside of the atomic medium is negligible, any amplitude and phase features formed inside the nonlinear medium are preserved outside, and can be detected in the form of photon number and phase correlations. The third-order photon correlation function has been measured previously in coupled atom-cavity and quantum dot-cavity systems, as well as in non-classical states of three photons such as the Greenberger-Horne-Zeilinger (GHZ) and ‘N00N’ states (12). In our approach, we split the light onto three single-photon counting modules. Furthermore, by mixing a detuned local oscillator (LO) into the final beamsplitter, we can also perform a heterodyne measurement in one of the detection arms (Fig. 1A). To connect the observed correlations to the physics of interacting Rydberg polaritons, we consider a state containing up to three photons,

where and a^†(t) is the photon creation operator of the time bin mode t. The correlation functions can be related to the wavefunctions as and . We refer to the phase of the N-photon wavefunction ψ_N as the N-photon phase, namely, , , and . The N-photon phase is obtained from the phase of the beat note signal on the third detector, conditioned on having observed N-1 photons in the other two detectors. The conditional phase relative to N uncorrelated photons, i.e. the nonlinear part of the phase, is denoted as ϕ^(N) (Fig. 3).

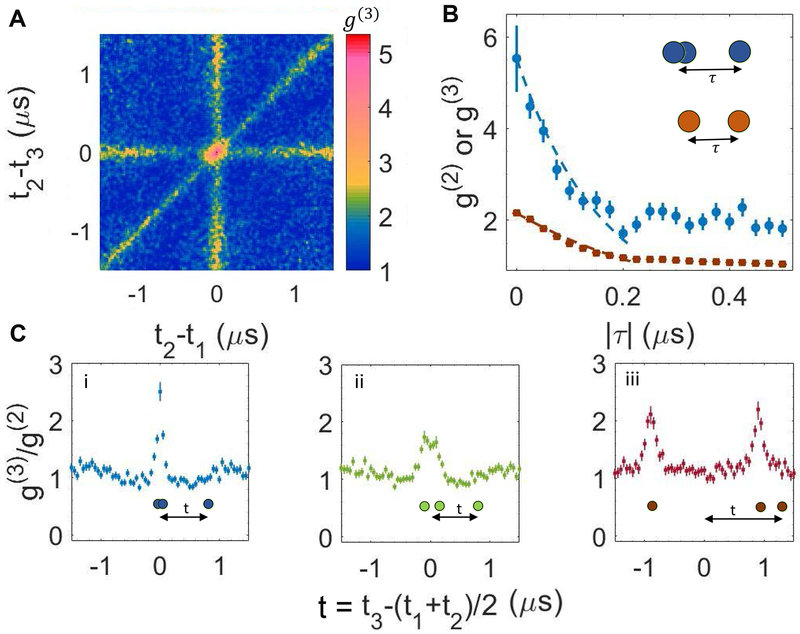
The experimentally measured g⁽³⁾ function (Fig. 2A, B) displays a clear bunching feature: the probability to detect three photons within a short time (≲ 25 ns) of one another is six times larger than for non-interacting photons in a laser beam. The increase at t₁ = t₂ = t₃ is accompanied by a depletion region for photons arriving within ~ 0.7 μs of one another, particularly visible along the lines of two-photon correlations t_i = t_j ≠ t_k (Fig. 2A): This depletion region is caused by the inflow of probability current towards the center t₁ = t₂ = t₃. Figure 2B compares the two-photon correlation function g⁽²⁾(t,t+|τ|) to that for three photons of which two photons were detected in the same time bin, g⁽³⁾(t,t,t + |τ|). The trimer feature is approximately a factor of 2 narrower than the dimer feature, showing that a photon is attracted more strongly to two other photons than to one. Figure 2C illustrates the binding of a third photon to two photons that are detected with a time separation T. If T exceeds the dimer time scale τ₂, then the third photon binds independently to either photon, while for T < τ₂ the two peaks merge into a single, more tightly bound trimer. This is analogous to the binding of a particle to a double-well potential as the distance between the wells is varied, since the polaritons can be approximately described as interacting massive particles moving at finite group velocity (6).

The dispersive and distance-dependent photon-photon interaction also manifests itself in a large conditional phase shift that depends on the time interval τ between the detection of the conditioning photons (at times t₁ = t₂ = t) and the phase measurement on detector D₃ at time t₃. We observe a conditional phase shift ϕ⁽³⁾ (t,t,t + |τ|) for the trimer near τ = 0 (Fig. 3A) that is significantly larger than the dimer phase shift ϕ⁽²⁾ (t,t+|τ|) (Fig. 3B). This confirms the stronger interaction between a photon and a dimer compared to that between one photon and another.

To understand these results quantitatively, we apply an effective field theory (EFT) (21) which describes the low-energy scattering of Rydberg polaritons. This EFT gives us a one-dimensional slow-light Hamiltonian density with a contact interaction.

where v_g is the group velocity inside the medium, is the effective photon mass, a is the scattering length, Ω_c is the control laser Rabi frequency, and Δ is the one-photon detuning. For weak interactions, (21,22). The single-mode, 1D approximation is justified by the small size of the probe waist compared to the blockade radius (r_B), while the corresponding Rayleigh range is similar to the atomic cloud size (with both being much larger than r_B). The latter condition implies that the incoming light has small transverse momenta components, while the former condition ensures that the dominant scattering occurs co-linearly with the probe beam. Combined with the large effective transverse mass in this system (23), the residual transverse dynamics arising from interactions are effectively frozen out on the timescale of the experiment [see also Ref. (6,15,18,24)]. In the limit where the average longitudinal distance between photons is larger than r_B, such that the low-momentum approximation underlying the EFT is valid, the 1D contact model provides an accurate description whenever a ≫ r_B, the microscopic range of the two-body potential. For our parameters, we find this is well satisfied as a ≳ 10r_B. is a quantum field annihilation operator, which corresponds to a photon outside the medium and a Rydberg polariton inside. Note that for our blue-detuned probe, the effective mass is negative and the interaction is repulsive. This situation maps onto a system with a positive mass and attractive interaction. The bound states can be determined from the exact solution of this model for finite particle numbers (25,26), resulting in the correlation functions and .

In the case t₁ = t₂ = t, we find that , implying that the width of three-photon wave-packet (corresponding to g⁽³⁾) is half that of g⁽²⁾ for the same experimental conditions, in good agreement with experimental observations. We calculate a/(2v_g) = 0.32 μs for our measured experimental parameters (27) and find it to be consistent with data (Fig. 2B, dashed lines). Following the quantum quench at the entry of the medium, the initial state is decomposed into the bound state and the continuum of scattering states (6). Near τ = 0, the scattering states dephase with each other, while the bound state propagates without distortion (27). This leads to a small contribution of scattering states in this region, with the bound state dominating the g⁽³⁾ function. The observed value of g⁽³⁾(0) is not universal, as it is affected by the contributions from long-wavelength scattering states and nonlinear losses in the system and, therefore, depends on the atomic density profile of the medium. The dimer and trimer binding energies can be estimated as and E₃ = 4E₂, respectively. This binding energy is ~ 10¹⁰ times smaller than in diatomic molecules such as NaCl and H₂, but is comparable to Feshbach (28) and Efimov (29) bound states of atoms with similar mass m and scattering length a. To further characterize the three-photon bound state, it is instructive to consider the phase ratio ϕ⁽³⁾ / ϕ⁽²⁾. For the bound-state contribution to the conditional phase ϕ⁽³⁾ (t, t, t)(ϕ⁽²⁾ (t, t)), the Hamiltonian of Eq.2 predicts a phase that equals the trimer binding energy times the propagation time in the medium. Thus from the bound state contributions, one would expect a ratio ϕ⁽³⁾ / ϕ⁽²⁾ = 4, independent of the atom-light detuning Δ. While the observed ratio (Fig. 4B) is approximately constant, it is smaller than 4.

The observed deviation is likely due to the two contributions of comparable magnitude.

One correction arises from the scattering states, or equivalently, from the fact that our Rydberg medium (~130 μm) is comparable in size to the two-photon bound state (~280 μm). For a medium that is short compared to the bound state, one expects the ratio to be 3, consistent with a dispersionless Kerr medium (30). The other, more fundamental correction, may be due to a contribution that does not arise from pairwise interactions, effectively representing a three-photon force. Specifically, when all three photons are within one blockade radius of one another, there can be only one Rydberg excitation and the potential cannot exceed the value corresponding to that of two photons (21,31). This saturation effect manifests itself as a short-range repulsive effective three-photon force which, according to our theoretical analysis (27), results in a reduction of ϕ⁽³⁾ / ϕ⁽²⁾ below 3. The corresponding correction to the bound state is smaller in the weakly interacting regime relevant to these experiments (31). This explains why the effective three-photon force has a relatively weak effect on the bunching of g⁽³⁾(|τ| < 0.2 μs), which is dominated by the bound state. Note that both the scaling arguments and numerical evidence indicate that the effective three-photon force contributes to the three-body scattering amplitudes more strongly than two-body finite range effects in this regime (21).

To quantitatively understand these effects, the EFT is modified to include the estimated effective three-photon force (27). Using the modified EFT, we compare the results with and without the repulsive effective three-photon force, while also taking into account the effects due to finite medium (Fig. 4B). Including this three-photon saturation force allows the phase ratio ϕ⁽³⁾ / ϕ⁽²⁾ to go below 3, in a reasonable agreement with the experimental observations. For fully saturated interactions between the polaritons, the interaction potential does not increase with photon number, and the phase ratio should approach 2.

The observation of the three-photon bound state, which can be viewed as photonic solitons in the quantum regime (7,8), can be extended along several different directions. First, increasing the length of the medium at constant atomic density would remove the effect of the scattering states through destructive quantum interference to larger τ and retain only the solitonic bound-state component. Additionally, the strong observed rate dependence of ϕ⁽³⁾ may indicate that larger photonic molecules and photonic clusters could be observed with improved detection efficiency and data acquisition rate. Furthermore, using an elliptical or larger round probe beam and carefully engineering the mass along different directions, the system can be extended to two and three dimensions, possibly permitting the observation of photonic Efimov states (32,33). Finally, our medium only supports one two/three-photon bound state, corresponding to a nonlinear phase less than π. A threefold increase in the atomic density would render the interaction potential sufficiently deep for a second bound state to appear near zero energy, which should result in resonant photon-photon scattering and a tunable scattering length (22). The presence of large effective N-body forces in this system opens intriguing possibilities to study exotic many-body phases of light and matter, including self-organization in open quantum systems (34,35), and quantum materials that cannot be realized with conventional systems.