Extreme value theorem

This article is about the calculus concept. For the statistical concept, see Fisher–Tippett–Gnedenko theorem.

A continuous function $f(x)$ on the closed interval $[a,b]$ showing the absolute max (red) and the absolute min (blue).

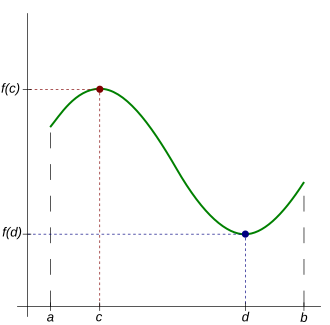
In real analysis, a branch of mathematics, the extreme value theorem states that if a real-valued function $f$ is continuous on the closed and bounded interval $[a,b]$, then $f$ must attain a maximum and a minimum, each at least once. That is, there exist numbers $c$ and $d$ in $[a,b]$ such that: $$f(c)\leq f(x)\leq f(d)\quad \forall x\in [a,b].$$

The extreme value theorem is more specific than the related boundedness theorem, which states merely that a continuous function $f$ on the closed interval $[a,b]$ is bounded on that interval; that is, there exist real numbers $m$ and $M$ such that: $$m\leq f(x)\leq M\quad \forall x\in [a,b].$$

This does not say that $M$ and $m$ are necessarily the maximum and minimum values of $f$ on the interval $[a,b],$ which is what the extreme value theorem stipulates must also be the case.

The extreme value theorem is used to prove Rolle's theorem. In a formulation due to Karl Weierstrass, this theorem states that a continuous function from a non-empty compact space to a subset of the real numbers attains a maximum and a minimum.

History

The extreme value theorem was originally proven by Bernard Bolzano in the 1830s in a work Function Theory but the work remained unpublished until 1930. Bolzano's proof consisted of showing that a continuous function on a closed interval was bounded, and then showing that the function attained a maximum and a minimum value. Both proofs involved what is known today as the Bolzano–Weierstrass theorem.

Functions to which the theorem does not apply

The following examples show why the function domain must be closed and bounded in order for the theorem to apply. Each fails to attain a maximum on the given interval.

1. $f(x)=x$ defined over $[0,\infty )$ is not bounded from above.
2. $f(x)={\frac {x}{1+x}}$ defined over $[0,\infty )$ is bounded from below but does not attain its least upper bound $1$.
3. $f(x)={\frac {1}{x}}$ defined over $(0,1]$ is not bounded from above.
4. $f(x)=1-x$ defined over $(0,1]$ is bounded but never attains its least upper bound $1$.

Defining $f(0)=0$ in the last two examples shows that both theorems require continuity on $[a,b]$.

Generalization to metric and topological spaces

When moving from the real line $\mathbb {R}$ to metric spaces and general topological spaces, the appropriate generalization of a closed bounded interval is a compact set. A set $K$ is said to be compact if it has the following property: from every collection of open sets $U_{\alpha }$ such that ${\textstyle \bigcup U_{\alpha }\supset K}$, a finite subcollection $U_{\alpha _{1}},\ldots ,U_{\alpha _{n}}$can be chosen such that ${\textstyle \bigcup _{i=1}^{n}U_{\alpha _{i}}\supset K}$. This is usually stated in short as "every open cover of $K$ has a finite subcover". The Heine–Borel theorem asserts that a subset of the real line is compact if and only if it is both closed and bounded. Correspondingly, a metric space has the Heine–Borel property if every closed and bounded set is also compact.

The concept of a continuous function can likewise be generalized. Given topological spaces $V,\ W$, a function $f:V\to W$ is said to be continuous if for every open set $U\subset W$, $f^{-1}(U)\subset V$ is also open. Given these definitions, continuous functions can be shown to preserve compactness:

Theorem—If $V,\ W$ are topological spaces, $f:V\to W$ is a continuous function, and $K\subset V$ is compact, then $f(K)\subset W$ is also compact.

In particular, if $W=\mathbb {R}$, then this theorem implies that $f(K)$ is closed and bounded for any compact set $K$, which in turn implies that $f$ attains its supremum and infimum on any (nonempty) compact set $K$. Thus, we have the following generalization of the extreme value theorem:

Theorem—If $K$ is a nonempty compact set and $f:K\to \mathbb {R}$ is a continuous function, then $f$ is bounded and there exist $p,q\in K$ such that $f(p)=\sup _{x\in K}f(x)$ and $f(q)=\inf _{x\in K}f(x)$.

Slightly more generally, this is also true for an upper semicontinuous function. (see compact space#Functions and compact spaces).

Proving the theorems

We look at the proof for the upper bound and the maximum of $f$. By applying these results to the function $-f$, the existence of the lower bound and the result for the minimum of $f$ follows. Also note that everything in the proof is done within the context of the real numbers.

We first prove the boundedness theorem, which is a step in the proof of the extreme value theorem. The basic steps involved in the proof of the extreme value theorem are:

1. Prove the boundedness theorem.
2. Find a sequence so that its image converges to the supremum of $f$.
3. Show that there exists a subsequence that converges to a point in the domain.
4. Use continuity to show that the image of the subsequence converges to the supremum.

Proof of the boundedness theorem

Boundedness Theorem—If $f(x)$ is continuous on $[a,b],$ then it is bounded on $[a,b].$

Proof

Suppose the function $f$ is not bounded above on the interval $[a,b]$. Pick a sequence $(x_{n})_{n\in \mathbb {N} }$ such that $x_{n}\in [a,b]$ and $f(x_{n})>n$. Because $[a,b]$ is bounded, the Bolzano–Weierstrass theorem implies that there exists a convergent subsequence $(x_{n_{k}})_{k\in \mathbb {N} }$ of $({x_{n}})$. Denote its limit by $x$. As $[a,b]$ is closed, it contains $x$. Because $f$ is continuous at $x$, we know that $f(x_{{n}_{k}})$ converges to the real number $f(x)$ (as $f$ is sequentially continuous at $x$). But $f(x_{{n}_{k}})>n_{k}\geq k$ for every $k$, which implies that $f(x_{{n}_{k}})$ diverges to $+\infty$, a contradiction. Therefore, $f$ is bounded above on $[a,b]$. ∎

Alternative proof

Consider the set $B$ of points $p$ in $[a,b]$ such that $f(x)$ is bounded on $[a,p]$. We note that $a$ is one such point, for $f(x)$ is bounded on $[a,a]$ by the value $f(a)$. If $e>a$ is another point, then all points between $a$ and $e$ also belong to $B$. In other words $B$ is an interval closed at its left end by $a$.

Now $f$ is continuous on the right at $a$, hence there exists $\delta >0$ such that $|f(x)-f(a)|<1$ for all $x$ in $[a,a+\delta ]$. Thus $f$ is bounded by $f(a)-1$ and $f(a)+1$ on the interval $[a,a+\delta ]$ so that all these points belong to $B$.

So far, we know that $B$ is an interval of non-zero length, closed at its left end by $a$.

Next, $B$ is bounded above by $b$. Hence the set $B$ has a supremum in $[a,b]$ ; let us call it $s$. From the non-zero length of $B$ we can deduce that $s>a$.

Suppose $s<b$. Now $f$ is continuous at $s$, hence there exists $\delta >0$ such that $|f(x)-f(s)|<1$ for all $x$ in $[s-\delta ,s+\delta ]$ so that $f$ is bounded on this interval. But it follows from the supremacy of $s$ that there exists a point belonging to $B$, $e$ say, which is greater than $s-\delta /2$. Thus $f$ is bounded on $[a,e]$ which overlaps $[s-\delta ,s+\delta ]$ so that $f$ is bounded on $[a,s+\delta ]$. This however contradicts the supremacy of $s$.

We must therefore have $s=b$. Now $f$ is continuous on the left at $s$, hence there exists $\delta >0$ such that $|f(x)-f(s)|<1$ for all $x$ in $[s-\delta ,s]$ so that $f$ is bounded on this interval. But it follows from the supremacy of $s$ that there exists a point belonging to $B$, $e$ say, which is greater than $s-\delta /2$. Thus $f$ is bounded on $[a,e]$ which overlaps $[s-\delta ,s]$ so that $f$ is bounded on $[a,s]$.   ∎

Proofs of the extreme value theorem

Proof of the Extreme Value Theorem

By the boundedness theorem, f is bounded from above, hence, by the Dedekind-completeness of the real numbers, the least upper bound (supremum) M of f exists. It is necessary to find a point d in [a, b] such that M = f(d). Let n be a natural number. As M is the least upper bound, M − 1/n is not an upper bound for f. Therefore, there exists d_n in [a, b] so that M − 1/n < f(d_n). This defines a sequence {d_n}. Since M is an upper bound for f, we have M − 1/n < f(d_n) ≤ M for all n. Therefore, the sequence {f(d_n)} converges to M.

The Bolzano–Weierstrass theorem tells us that there exists a subsequence {$d_{n_{k}}$}, which converges to some d and, as [a, b] is closed, d is in [a, b]. Since f is continuous at d, the sequence {f($d_{n_{k}}$)} converges to f(d). But {f(d_nk)} is a subsequence of {f(d_n)} that converges to M, so M = f(d). Therefore, f attains its supremum M at d.  ∎

Alternative Proof of the Extreme Value Theorem

The set {y ∈ R : y = f(x) for some x ∈ [a,b]} is a bounded set. Hence, its least upper bound exists by least upper bound property of the real numbers. Let M = sup(f(x)) on [a, b]. If there is no point x on [a, b] so that f(x) = M, then f(x) < M on [a, b]. Therefore, 1/(M − f(x)) is continuous on [a, b].

However, to every positive number ε, there is always some x in [a, b] such that M − f(x) < ε because M is the least upper bound. Hence, 1/(M − f(x)) > 1/ε, which means that 1/(M − f(x)) is not bounded. Since every continuous function on [a, b] is bounded, this contradicts the conclusion that 1/(M − f(x)) was continuous on [a, b]. Therefore, there must be a point x in [a, b] such that f(x) = M. ∎

Proof using the hyperreals

Proof

In the setting of non-standard calculus, let N  be an infinite hyperinteger. The interval [0, 1] has a natural hyperreal extension. Consider its partition into N subintervals of equal infinitesimal length 1/N, with partition points x_i = i /N as i "runs" from 0 to N. The function ƒ  is also naturally extended to a function ƒ* defined on the hyperreals between 0 and 1. Note that in the standard setting (when N  is finite), a point with the maximal value of ƒ can always be chosen among the N+1 points x_i, by induction. Hence, by the transfer principle, there is a hyperinteger i₀ such that 0 ≤ i₀ ≤ N and $f^{*}(x_{i_{0}})\geq f^{*}(x_{i})$  for all i = 0, ..., N. Consider the real point $$c=\mathbf {st} (x_{i_{0}})$$ where st is the standard part function. An arbitrary real point x lies in a suitable sub-interval of the partition, namely $x\in [x_{i},x_{i+1}]$, so that  st(x_i) = x. Applying st to the inequality $f^{*}(x_{i_{0}})\geq f^{*}(x_{i})$, we obtain $\mathbf {st} (f^{*}(x_{i_{0}}))\geq \mathbf {st} (f^{*}(x_{i}))$. By continuity of ƒ  we have

$\mathbf {st} (f^{*}(x_{i_{0}}))=f(\mathbf {st} (x_{i_{0}}))=f(c)$.

Hence ƒ(c) ≥ ƒ(x), for all real x, proving c to be a maximum of ƒ. ∎

Proof from first principles

Statement      If $f(x)$ is continuous on $[a,b]$ then it attains its supremum on $[a,b]$

Proof

By the Boundedness Theorem, $f(x)$ is bounded above on $[a,b]$ and by the completeness property of the real numbers has a supremum in $[a,b]$. Let us call it $M$, or $M[a,b]$. It is clear that the restriction of $f$ to the subinterval $[a,x]$ where $x\leq b$ has a supremum $M[a,x]$ which is less than or equal to $M$, and that $M[a,x]$ increases from $f(a)$ to $M$ as $x$ increases from $a$ to $b$.

If $f(a)=M$ then we are done. Suppose therefore that $f(a)<M$ and let $d=M-f(a)$. Consider the set $L$ of points $x$ in $[a,b]$ such that $M[a,x]<M$.

Clearly $a\in L$ ; moreover if $e>a$ is another point in $L$ then all points between $a$ and $e$ also belong to $L$ because $M[a,x]$ is monotonic increasing. Hence $L$ is a non-empty interval, closed at its left end by $a$.

Now $f$ is continuous on the right at $a$, hence there exists $\delta >0$ such that $|f(x)-f(a)|<d/2$ for all $x$ in $[a,a+\delta ]$. Thus $f$ is less than $M-d/2$ on the interval $[a,a+\delta ]$ so that all these points belong to $L$.

Next, $L$ is bounded above by $b$ and has therefore a supremum in $[a,b]$: let us call it $s$. We see from the above that $s>a$. We will show that $s$ is the point we are seeking i.e. the point where $f$ attains its supremum, or in other words $f(s)=M$.

Suppose the contrary viz. $f(s)<M$. Let $d=M-f(s)$ and consider the following two cases:

1. $s<b$.   As $f$ is continuous at $s$, there exists $\delta >0$ such that $|f(x)-f(s)|<d/2$ for all $x$ in $[s-\delta ,s+\delta ]$. This means that $f$ is less than $M-d/2$ on the interval $[s-\delta ,s+\delta ]$. But it follows from the supremacy of $s$ that there exists a point, $e$ say, belonging to $L$ which is greater than $s-\delta$. By the definition of $L$, $M[a,e]<M$. Let $d_{1}=M-M[a,e]$ then for all $x$ in $[a,e]$, $f(x)\leq M-d_{1}$. Taking $d_{2}$ to be the minimum of $d/2$ and $d_{1}$, we have $f(x)\leq M-d_{2}$ for all $x$ in $[a,s+\delta ]$.
   Hence $M[a,s+\delta ]<M$ so that $s+\delta \in L$. This however contradicts the supremacy of $s$ and completes the proof.
2. $s=b$.   As $f$ is continuous on the left at $s$, there exists $\delta >0$ such that $|f(x)-f(s)|<d/2$ for all $x$ in $[s-\delta ,s]$. This means that $f$ is less than $M-d/2$ on the interval $[s-\delta ,s]$. But it follows from the supremacy of $s$ that there exists a point, $e$ say, belonging to $L$ which is greater than $s-\delta$. By the definition of $L$, $M[a,e]<M$. Let $d_{1}=M-M[a,e]$ then for all $x$ in $[a,e]$, $f(x)\leq M-d_{1}$. Taking $d_{2}$ to be the minimum of $d/2$ and $d_{1}$, we have $f(x)\leq M-d_{2}$ for all $x$ in $[a,b]$. This contradicts the supremacy of $M$ and completes the proof. ∎

Extension to semi-continuous functions

If the continuity of the function f is weakened to semi-continuity, then the corresponding half of the boundedness theorem and the extreme value theorem hold and the values −∞ or +∞, respectively, from the extended real number line can be allowed as possible values.

A function $f:[a,b]\to [-\infty ,\infty )$ is said to be upper semi-continuous if $$\limsup _{y\to x}f(y)\leq f(x)\quad \forall x\in [a,b].$$

Theorem—If a function f : [a, b] → [–∞, ∞) is upper semi-continuous, then f is bounded above and attains its supremum.

Proof

If $f(x)=-\infty$ for all x in [a,b], then the supremum is also $-\infty$ and the theorem is true. In all other cases, the proof is a slight modification of the proofs given above. In the proof of the boundedness theorem, the upper semi-continuity of f at x only implies that the limit superior of the subsequence {f(x_nk)} is bounded above by f(x) < ∞, but that is enough to obtain the contradiction. In the proof of the extreme value theorem, upper semi-continuity of f at d implies that the limit superior of the subsequence {f(d_nk)} is bounded above by f(d), but this suffices to conclude that f(d) = M. ∎

Applying this result to −f proves a similar result for the infimums of lower semicontinuous functions. A function $f:[a,b]\to [-\infty ,\infty )$ is said to be lower semi-continuous if $$\liminf _{y\to x}f(y)\geq f(x)\quad \forall x\in [a,b].$$

Theorem—If a function f : [a, b] → (–∞, ∞] is lower semi-continuous, then f is bounded below and attains its infimum.

A real-valued function is upper as well as lower semi-continuous, if and only if it is continuous in the usual sense. Hence these two theorems imply the boundedness theorem and the extreme value theorem.

Further reading

• Adams, Robert A. (1995). Calculus : A Complete Course. Reading: Addison-Wesley. pp. 706–707. ISBN 0-201-82823-5.
• Protter, M. H.; Morrey, C. B. (1977). "The Boundedness and Extreme–Value Theorems". A First Course in Real Analysis. New York: Springer. pp. 71–73. ISBN 0-387-90215-5.

External links

• A Proof for extreme value theorem at cut-the-knot
• Extreme Value Theorem by Jacqueline Wandzura with additional contributions by Stephen Wandzura, the Wolfram Demonstrations Project.
• Weisstein, Eric W. "Extreme Value Theorem". MathWorld.
• Mizar system proof: http://mizar.org/version/current/html/weierstr.html#T15